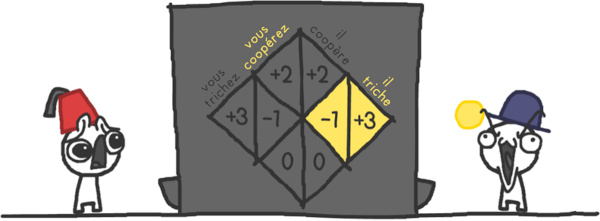
Le domaine des mathématiques s’intéressant à l’étude des modèles mathématiques des interactions stratégiques entre des agents rationnels est la théorie des jeux. Le dilemme du prisonnier caractérise en théorie des jeux une situation dans laquelle les intérêts individuels s’opposent aux intérêts collectifs, mais où, en l'absence de communication entre les deux agents, chacun choisira de trahir l'autre. En voici sa formulation classique :

Deux suspects sont arrêtés par la police. Mais les agents n'ont pas assez de preuves pour les inculper, donc ils les interrogent séparément en leur faisant l’offre suivante : « Si tu dénonces ton complice et qu'il ne te dénonce pas, tu seras remis en liberté et l'autre écopera de 10 ans de prison. Si tu le dénonces et lui aussi, vous écoperez tous les deux de 5 ans de prison. Si personne ne dénonce l'autre, vous aurez tous deux 6 mois de prison. »

Dans cette présentation, on analysera mathématiquement cette situation et ses variantes tout en effectuant plusieurs simulations entre nous et à l’ordinateur. On verra aussi de multiples manifestations de ce dilemme dans des domaines variés comme l'économie, la biologie de l’évolution, la politique internationale, les politiques commerciales, la psychologie, le traitement médiatique de la rumeur, le sport, les études environnementales et même l'émergence de règles morales dans des communautés. Alors, allez-vous coopérer ou trahir ? Bon jeu !

Fichier de présentation.